Let's build GPT:from scratch, in code, spelled out.
本文是我对 Andrej Karpathy 大佬手搓 GPT 的经典视频的自学笔记。
《Let's build GPT:from scratch, in code, spelled out.》是 Andrej Karpathy 大佬录制的课程,该课程约 2 小时,从头构建出一个可工作的 GPT,Talk is Cheap,show me the Code,相当硬核。完成该课程,理论与实践会同时打下坚实基础,这也是我选择自学它的原因。我用 yt-dlp 下载该课程视频及网站自动识别字幕,网站自动识别字幕并不完全准确。在 B 站上有搬运视频,字幕更加准确,我更加推荐。
学习材料
我自学起来相当吃力。好在有 ChatGPT,以及互联网上丰富的文章教学资源,如有神助,帮助我得以了解他们。本节我梳理对我有所帮助的学习材料:
- 《Create GPT from scratch using Python — Part 1》:这篇文章帮助我度过了课程的前40分钟,是对视频内容非常好的文字补充描述。但是可惜的是,作者只写了 Part1,未写 Part2。该作者的其它文章,也同样值得推荐。
- 《jjchen1》:这是一个为期 30 天的 LLM 专题研究笔记,并且是中文笔记,其中 Day2、Day3 对该视频进行了详细介绍。该作者的其它文章同样值得推荐,主要是研究在一张 3090 显卡下,能对 LLM 进行哪些训练,有很强的实战性。
另外,笔记中有诸多截图、图片,引用自这些课程、视频,在此统一注明出处。
基础概念
在本节中,我梳理了一些基础概念,这些概念有助于我们对视频的理解。
Andrej Karpathy
援引 jjchen1 对 Andrej Karpathy 大佬的介绍:
Andrej Karpathy 不仅对 OpenAI 和特斯拉有重要影响,也是深度学习社区的重要人物。他能够清晰、详细地表达他的思维方式,并且能根据自己的理解,简化复杂的模型,并最终复现(如 GPT、LLama2)。
这种讲述方法,能够让像我这样的门外汉,有机会深入其中,深入了解这些前沿技术。
Transformer 模型
2017 年论文《Attention is All You Need》提出了 Transformer模型。GPT 的全称是 Generative Pretrained Transformer 生成式预训练 Transformer 模型。这篇论文开启了近年来 AI 的迅猛发展。
《Let's build GPT》视频目标:训练一个基于 Transformer 模型的语言模型。教育目的。使用更小的数据集(Tiny Shakespeare,1.06MB)。对应的 GitHub 项目是 nanoGPT。Andrej Karpathy 大佬带你,手把手,从零开始写一个 nanoGPT。
ChatGPT
ChatGPT 是由 OpenAI 推出的(最早)基于 GPT-3 模型的大型语言模型。最新高级版本基于 GPT-4。ChatGPT 基于海量数据和算力进行训练,并且采用高超的训练技巧,处于业界领先地位。
但就本质而言,ChatGPT 也是语言模型,核心原理是相同的:ChatGPT 将用户输入(Prompt,提示)分解为一系列词元(Token),然后使用这个序列来预测下一个最有可能的单词或者一系列单词,以类似人类的方式完成提示。
基于字符级别的语言模型
《Let's build GPT》中训练的语言模型,处于教学目的,是一种基于字符级别的语言模型(character level language model)。所谓基于字符级别,是根据前面的字符(字母),来预测下一个字母。
这与现实中的语言模型不同,现实中的语言模型(如 ChatGPT)是基于 Token 的语言模型。根据前面的 Token(可简单理解为单词)预测下一个单词。
这里使用字符级别,是因为结合 Tiny Shakespeare 语料理解起来比较直观。显然基于 Token 的语言模型更加高级、强大。
下图是基于字符级别的语言模型的示意图:
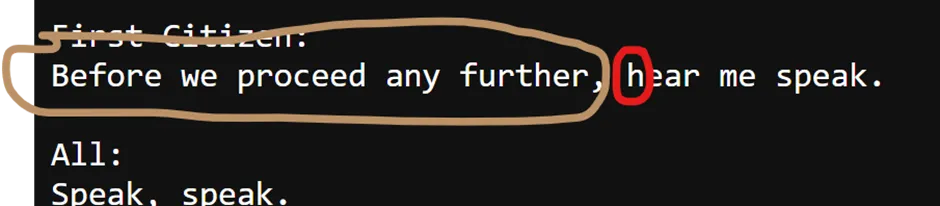
假设用户输入下面这段话:“Before we proceed any further”,字符级别的语言模型将根据前面的字母尝试预测下一个字母 h。
nanoGPT
nanoGPT 也是 Andrej Karpathy 开发的开源项目,它是一个用于训练/微调中等规模 GPT 模型的最简单、最快速的方案。它是对 minGPT 的改写,更注重实用性而不是理论教育。项目地址:karpathy/nanoGPT
目前 nanoGPT 已经能在 OpenWebText 数据集上重现 GPT-2(124M)模型,仅需在单个 8xA100 40GB 节点上运行约 4 天的时间。代码本身简洁明了,可以选择从 OpenAI 加载 GPT-2 的权重。目前仍在积极开发中,
Step1:数据集准备
理论铺垫完成,接下来按照视频内容,进入实战环节。在后面的章节中,我将按照视频内容以及其他学习材料,将视频内容动手实践一遍,并尽可能详细地记录中间过程。
注:接下来的代码运行在 Jupyter Notebook 中。
首先下载数据集:
# We always start with a dataset to train on. Let's download the tiny shakespeare dataset
!wget https://raw.githubusercontent.com/karpathy/char-rnn/master/data/tinyshakespeare/input.txt
读取 Tiny Shakespeare 数据集,并打印数据集长度:
# read it in to inspect it
with open('input.txt', 'r', encoding='utf-8') as f:
text = f.read()
print("length of dataset in characters: ", len(text))
# 结果:
length of dataset in characters: 1115394
统计数据集中都包含哪些字符种类:
# here are all the unique characters that occur in this text
chars = sorted(list(set(text)))
vocab_size = len(chars)
print(''.join(chars))
print(vocab_size)
# 结果:
!{{CODE_BLOCK_2}}',-.3:;?ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz
65
其中 vocab_size 表示 Tiny Shakespeare 由 65 种字符构成。chars 则是他们的具体内容。这些字符是模型能看到并生成的。
Step2:Tokenize
Tokenize 指的是,将原始文本转化为一些数值的序列,即 Token 序列。
如何将自然语言文本变为 Token 序列,有很多高级算法,比如:google/sentencepiece、openai/tiktoken。
前面说到,本文中采用的基于字符级别的语言模型,它的 Tokennizer 算法十分简单。前面代码中的 chars 包含了语料中所有字符的种类,给出一个字符,只要看该字符在 chars 中的 indexOf,就得到了一种数值化的方法。
将上面的词汇表(chars)映射为整数。stoi 字符到整数的映射,itos 整数到字符的映射。encode 和 decode 分别是对字符串的编解码。
# create a mapping from characters to integers
stoi = { ch:i for i,ch in enumerate(chars) }
itos = { i:ch for i,ch in enumerate(chars) }
encode = lambda s: [stoi[c] for c in s] # encoder: take a string, output a list of integers
decode = lambda l: ''.join([itos[i] for i in l]) # decoder: take a list of integers, output a string
print(encode("hii there"))
print(decode(encode("hii there")))
# 结果
[46, 47, 47, 1, 58, 46, 43, 56, 43]
hii there
在上面代码中,实现了一个编解码方法,能够将文本编码为 "Token" 序列。之所以 Token 要打引号,因为在基于字符级别的粒度下,算法直观但是过于简单。还有一点需要注意的是,接下来使用的自然语言,必须是 chars 中的字符,不能超出这个范围。
不论是高级算法还是本文中的简化方法:原理都是一样的,将文本转为数值序列。以 tiktoken(有 50257 种 Tokens)为例:
import tiktoken
enc = tiktoken.get_encoding('gpt2')
enc.n_vocab
# 50257
enc.encode('hii there')
# [71, 4178, 612]
enc.decode([71, 4178, 612])
# 'hii there'
可以看到,使用起来与本文是一样的。但是:
通过高级 Tokenizer 编码后,序列的长度变短。Tiny Shakespeare 要每个字符一个 Token,而语言模型的上下文有限,能够支持的 Token 长度也有限。因此高级的 Tokenizer,提升了表达原始信息的密度和效率。
接下来,将整个 Tiny Shakespeare 编码后,转为 PyTorch 序列:
# let's now encode the entire text dataset and store it into a torch.Tensor
import torch # we use PyTorch: https://pytorch.org
data = torch.tensor(encode(text), dtype=torch.long)
print(data.shape, data.dtype)
print(data[:1000]) # the 1000 characters we looked at earier will to the GPT look like this
Tensor 长这样:

Step3:训练集、验证集
Tiny Shakespeare 的前 90% 用于训练,后 10% 用于验证:
# Let's now split up the data into train and validation sets
n = int(0.9*len(data)) # first 90% will be train, rest val
train_data = data[:n]
val_data = data[n:]
所谓训练:指让语言模型从这些文本中学习规律。最理想情况下,语言模型学完 Tiny Shakespeare 后,犹如莎翁再世,出口成章。(实际上这是很难做到的,本文中构建的 GPT 模型,尽管已经非常强大,但仍处于 “说都不会话” 的阶段。
所谓验证:让训练好的模型,用最后的这 10% 的部分,以某种方法,让模型生成,然后对比生成内容与验证集中的验证内容的相似度。如果相似度高,说明模型已经自学成莎了,毕竟最后这 10% 它都没看过。如果相似度低,说明模型只学到了皮毛。
训练集怎么用?不是说把所有内容一次性传入 Transformer 模型。而是需要对数据进行分片(随机采样),每次对一个分片进行训练。
Step4:Block 数据切分
分片(Chunk)称之为 block,分片的大小称之为 block_size。以下是一个 Block 举例:
block_size = 8
train_data[:block_size+1]
# 结果
tensor([18, 47, 56, 57, 58, 1, 15, 47, 58])
这里取了训练集中的第一个 Block。block_size 大小为 8,为什么我们取了 9 个 Token 呢?
为了理解这个问题,首先看训练方式,将 Chunck 拆分为两个子集 x 和 y,其中 x 表示输入 Token 序列,在使用时是累增的,y 表示基于该输入,与其的输出。具体代码如下:
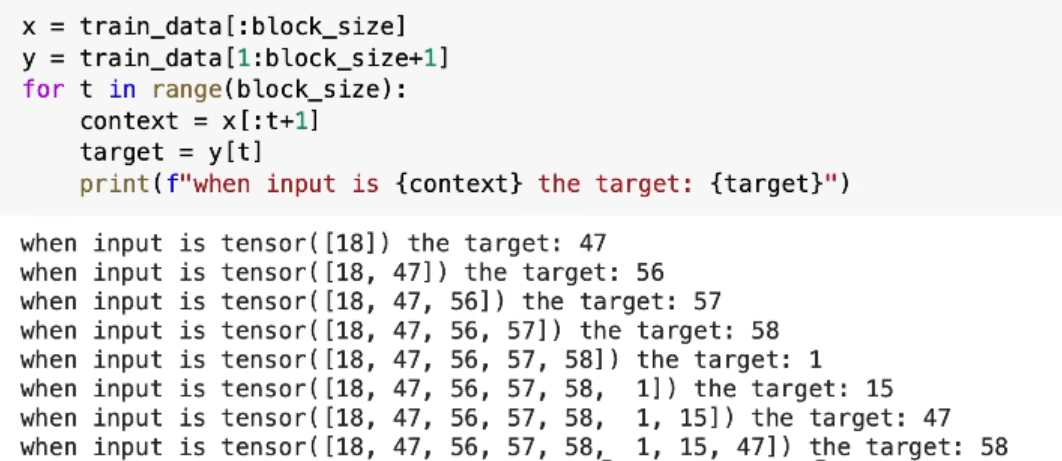
给出一个 Block,分为几轮。第一轮,用第一个 Token 推测第二个 Token。第二轮,用前两个 Token推测第三个 Token。以此类推,到了第八轮,用前八个 Token 推测第九个 Token。
block_size 大小为 8,表示我们的最大训练长度为 8。每一批数据有 9 个元素,其中第九个元素不参与训练,只参与验证。
我们将 Tiny Shakespeare 切分称一系列 Block,就相当于一系列考试题,每道题是一个长度为 9 的连续 Token 序列,按照上图方式,考语言模型。
为什么要以逐渐递增的方式,连同过程也加入训练?这是为了训练 Transformer 模型的过程推理能力。这样,依据有限输入,模型能够一步步自行推理下去。
Step5:Batch 划分
将训练集进行 Block 切分后,我们可以一个一个向 GPU 投喂(训练)。但是,我们想,GPU 什么能力最强大?并行计算能力!一个一个向 GPU 投喂喂不饱。为了能够充分发挥出 GPU 的并行运算能力,我们将多个 Block 打包成一批(Batch),一批一批向 GPU 投喂。总之一句话,不能让 GPU 闲着,提升训练效率。
值得一提的是,尽管一个 Batch 内的 Blocks 是一批进入 GPU 的,但是它们之间相互隔离,互相不知道对方的存在,互不干扰。
分批的代码实现如下:
torch.manual_seed(1337)
batch_size = 4 # how many independent sequences will we process in parallel?
block_size = 8 # what is the maximum context length for predictions?
def get_batch(split):
# generate a small batch of data of inputs x and targets y
data = train_data if split == 'train' else val_data
ix = torch.randint(len(data) - block_size, (batch_size,))
x = torch.stack([data[i:i+block_size] for i in ix])
y = torch.stack([data[i+1:i+block_size+1] for i in ix])
return x, y
xb, yb = get_batch('train')
print('inputs:')
print(xb.shape)
print(xb)
print('targets:')
print(yb.shape)
print(yb)
print('----')
for b in range(batch_size): # batch dimension
for t in range(block_size): # time dimension
context = xb[b, :t+1]
target = yb[b,t]
print(f"when input is {context.tolist()} the target: {target}")
从代码中可以看出:Block 的大小为 8。Batch 的大小为 4,即一个 Batch 包含 4 个 Blocks。另外锁定了随机数种子为 1337,这样我们都能复现跟 Andrej Karpathy 一样的训练效果。
上述代码,运行后的日志输出(部分截图)如下。可以看出:输入由 1 个 8 元素向量变为 4 个。验证向量也变为 4 个。都 Batch 化了。在后续的推理释义中,也是将 Batch 内每个 Block 的推理过程打印出来。

Step6:BigramLanguageModel V1
接下来 Andrej Karpathy 大佬开始实现起了 BigramLanguageModel。初学时,看到这里我有点懵:不是 Build GPT 吗?怎么拐弯儿了?GPT 里面也不包含 BigramLanguageModel 呀!
后来我才明白:BigramLanguageModel 是一个经典、简单、易于理解的框架,Andrej Karpathy 借助 BigramLanguageModel 先帮助我们把语言模型的大框架搭建起来。然后,在框架内,一步一步,添砖加瓦,一点点改出 GPT。妙啊!
二元语言模型(BigramLanguageModel),概括说:根据前一个词,来推测下一个词。举例来说:例如,对于句子 "I love to play football",会得到以下的词组:"I love", "love to", "to play", "play football"。
上面是二元情况,可以推广到 N-gram Langugage Model,其中 BigramLanguageModel 是
更多学习资料,可参见:《自然语言处理中N-Gram模型介绍》。
接下来,我们来实现第一个 BigramLanguageModel,与视频不同之处在于,我称之为 BigramLanguageModelV1,后续每进行一次更改,都会创建一个新类,并提升版本。
模型继承自 Pytorch 的 Module,在构造方法中声明模型内部包含的层。可见该模型只有一层(nn.Embedding)。模型还包括 forward,前向传播过程,用于训练。模型一旦训练好后,通过 generate 可进行文本生成。代码实现如下:
import torch
import torch.nn as nn
from torch.nn import functional as F
torch.manual_seed(1337)
# 二元语言模型实现
class BigramLanguageModelV1(nn.Module):
def __init__(self, vocab_size):
super().__init__()
# 每个词直接从一个查找表中获取下一个词的logits值
# logits是模型做出预测前的一组未经归一化的分数,反映了不同结果的相对可能性
self.token_embedding_table = nn.Embedding(vocab_size, vocab_size)
# 模型前向传播
# idx:即前面的 x,表示输入数据,词在词汇表中的索引的向量
# targets:训练的目标输出,比如正确的下一个词的索引
def forward(self, idx, targets=None):
# idx and targets are both (B,T) tensor of integers
logits = self.token_embedding_table(idx) # (B,T,C)
if targets is None:
loss = None
else:
B, T, C = logits.shape
logits = logits.view(B*T, C)
targets = targets.view(B*T)
loss = F.cross_entropy(logits, targets)
return logits, loss
# 在模型已经训练好之后,根据给定的输入生成文本的方法。
def generate(self, idx, max_new_tokens):
# idx is (B, T) array of indices in the current context
for _ in range(max_new_tokens):
# get the predictions
logits, loss = self(idx)
# focus only on the last time step
logits = logits[:, -1, :] # becomes (B, C)
# apply softmax to get probabilities
probs = F.softmax(logits, dim=-1) # (B, C)
# sample from the distribution
idx_next = torch.multinomial(probs, num_samples=1) # (B, 1)
# append sampled index to the running sequence
idx = torch.cat((idx, idx_next), dim=1) # (B, T+1)
return idx
下面对上述代码进行详细分析。
在构造函数中,声明了一个 nn.Embedding 层,我们用它实现了二元语言模型根据前一个词来推断下一个词的能力。具体是怎么实现的呢?
首先,nn.Embedding组件是 PyTorch 框架中用于词嵌入的一个模块。它接受两个参数:vocab_size(词汇表大小)和嵌入的维度。在这个例子中,嵌入的维度被设置为与词汇表的大小相同,这意味着每个词都会被映射到一个与整个词汇表大小相同的向量中。
上面这句高亮的话能看懂吗?坦白说,我是看不懂。所以,我决定先跑起来再说!在后续章节,先把模型跑起来,建立直观概念后,再回过头来攻克这里。
Step7:BigramLanguageModel V1 运行
值得一提的是,我们目前对 BigramLanguageModel 还没有进行任何训练。尽管我们搭建了 BigramLanguageModel 这个神经网络,但它目前处于神经错乱状态。
通过下面代码来运行一下神经错乱状态的模型,首先先从训练集中选取数据,选取 Block 长度为 8,获取 4 个批次。并创建模型实例,供后续使用:
torch.manual_seed(1337)
batch_size = 4 # 一批 4 个 Block
block_size = 8 # 一个 Block 序列长度为 8
# 随机选取批数据
def get_batch(split):
# generate a small batch of data of inputs x and targets y
data = train_data if split == 'train' else val_data
ix = torch.randint(len(data) - block_size, (batch_size,))
x = torch.stack([data[i:i+block_size] for i in ix])
y = torch.stack([data[i+1:i+block_size+1] for i in ix])
return x, y
xb, yb = get_batch('train')
print('inputs(xb):')
print(xb.shape)
print(xb)
print('targets(yb):')
print(yb.shape)
print(yb)
# get device
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# create model
m = BigramLanguageModelV1(vocab_size).to(device)
打印日志如下:
inputs(xb):
torch.Size([4, 8])
tensor([[24, 43, 58, 5, 57, 1, 46, 43],
[44, 53, 56, 1, 58, 46, 39, 58],
[52, 58, 1, 58, 46, 39, 58, 1],
[25, 17, 27, 10, 0, 21, 1, 54]])
targets(yb):
torch.Size([4, 8])
tensor([[43, 58, 5, 57, 1, 46, 43, 39],
[53, 56, 1, 58, 46, 39, 58, 1],
[58, 1, 58, 46, 39, 58, 1, 46],
[17, 27, 10, 0, 21, 1, 54, 39]])
对 xb 和 yb,我们是相当之熟悉了。下面进行一次前向传播,将得到 logits, loss:
logits, loss = m(xb.to(device),
yb.to(device))
print(logits.shape)
print(loss)
日志打印如下:
torch.Size([32, 65])
tensor(5.0364, grad_fn=<NllLossBackward0>)
logits 是模型做出预测前的一组未经归一化的分数,反映了不同结果的相对可能性。如何理解 logits 的 shape 呢?xb(4x8)的每个元素(Token,字母在词汇表中的排序),在 forward 中,都要输入 nn.Embedding,得到一个大小为 65(词汇表大小)的向量。该向量中的每个元素,表示有当前 Token,推测出该向量表示 Token 的可能性(未归一化)。
下面以第一个词为例,它的长度为 65 的表示 65 种字符可能性的向量为:
print(logits[0].shape)
print(logits[0])
打印结果:
torch.Size([65])
tensor([ 1.6347, -0.0518, 0.4996, 0.7216, 0.5085, -0.7719, 0.2388, 0.3138,
0.2178, 0.0328, -0.1699, 1.0659, 0.7200, -0.6166, 0.0806, 2.5231,
-1.4623, 2.1707, 0.1624, 1.0296, -1.1377, 0.5856, 0.0173, 0.3136,
1.0124, 1.5122, -0.3359, 0.2456, -0.3773, 0.1587, 2.1503, -1.5131,
-0.9552, -0.8995, -0.9583, -0.5945, 0.5850, 0.5266, 0.7615, 0.5331,
1.1796, 1.3316, -0.2094, 0.0960, -0.6945, 0.5669, -0.5883, 1.4064,
-1.2537, -1.5195, 0.7446, 1.1914, 0.1801, 1.2333, -0.2299, -0.1531,
0.8408, -0.3993, -0.6126, -0.6597, 0.5906, 1.1219, 0.2432, 1.1519,
0.9950], grad_fn=<SelectBackward0>)
其中,值最大的元素的序号,就是最可能的那个字母。注意,模型还没有进行任何训练,处于神经错乱状态,预测地与事实不符是正常的。
有了这个词嵌入向量后,计算出模型与 Target(事实的下一个 Token)之间的误差了。这里使用了交叉熵误差。
交叉熵误差(Cross-Entropy Loss,简称CE)是一种常用的损失函数(loss function),尤其在机器学习和深度学习中的分类问题。它是用来衡量模型预测概率分布与真实概率分布之间的相似度。交叉熵误差的值越小,表示模型预测的概率分布与真实概率分布越接近,模型的性能越好。
对于交叉熵误差,本文中暂不深究了。(点进交叉熵误差的笔记可看到计算公式,我暂时还不知道在本文场景下这是怎么算出来的。但是把它当作黑盒,不影响对本文的理解,总之它越小越好。)
注:在前文中说道,训练是累增的,第一轮用一个 Token 训练,第二轮用两个。从上面的 BigramLanguageModel V1 模型来看,没看出累增来。不记得前面的累增是什么?看看这堆日志回忆一下:
when input is [24] the target: 43
when input is [24, 43] the target: 58
when input is [24, 43, 58] the target: 5
when input is [24, 43, 58, 5] the target: 57
when input is [24, 43, 58, 5, 57] the target: 1
when input is [24, 43, 58, 5, 57, 1] the target: 46
when input is [24, 43, 58, 5, 57, 1, 46] the target: 43
when input is [24, 43, 58, 5, 57, 1, 46, 43] the target: 39
这种累增训练是用来训练 GPT 的,我们现在还处于 BigramLanguageModel 框架学习阶段。BigramLanguageModel 不按照这种方法训练,这里的训练方法是:给出一个 Token,预测下一个 Token,与实际下一个 Token 作对比,从中学习。Block 序列中,每个元素都参与这一训练过程
前向传播过程看完了,接下来尝试调用 generate 进行一次文本生成:
print(
decode(
m.generate(
idx = torch.zeros((1, 1), dtype=torch.long).to(device),
max_new_tokens=12)[0].tolist()))
其中,输入是一个 1x1 的零矩阵,这是原始输入。max_new_tokens 为 12 表示生成一个长度为 12 的文本。在 generate 内部有一个循环,每一轮预测出的 Token,会加入之前的结果,作为新输入。模型 generate 出来的是 Token,需要进行解码,变为自然语言。
运行后打印日志如下,全是乱码:
l-QYjt'CL?jL
下面梳理 generate 内的具体逻辑:
def generate(self, idx, max_new_tokens):
# 在本例中,输入 idx 初始值为 [0],max_new_tokens 为 12
# idx is (B, T) array of indices in the current context
# 循环预测,本轮预测值将作为下轮输入的一部分
for _ in range(max_new_tokens):
# 调用 forwards 产生一个预测
# 未传 targets,误差 loss 无意义
logits, loss = self(idx)
# 假设 idx = [元素1, 元素2, 元素3]
# logits 是对每个元素进行预测,shape 为 3x65
# 对元素1 和 元素2 的预测是无意义的
# 因为我们想要的是对元素3 的预测
# 下面:第一个 ":" 表示所有批次的
# 第二个 "-1" 表示最后一个元素的预测
# 第三个 ":" 表示大小为 65(词汇表大小)的预测向量
logits = logits[:, -1, :] # becomes (B, C)
# 使用 softmax,得到归一化的概率分布
probs = F.softmax(logits, dim=-1) # (B, C)
# 进行采样,采样值就是预测值
# 如果随机数种子未固定,每次采样结果都不同
# 本文中为了复现,固定了随机数种子
# sample from the distribution
idx_next = torch.multinomial(probs, num_samples=1) # (B, 1)
# append sampled index to the running sequence
# 将预测结果拼接到 idx 中,作为下一轮输入
idx = torch.cat((idx, idx_next), dim=1) # (B, T+1)
return idx
词嵌入
在 BigramLanguageModel 中,有一个非常重要的概念——词嵌入。
词向量(Word Vector),也被称为词嵌入(Word Embedding),是自然语言处理(NLP)和深度学习中的一种技术。它将词语转化为计算机可以理解的数值形式,即向量,使得计算机能够处理文本数据,是自然语言处理(NLP)中一种表示词汇的技术。
词向量的一个重要特性是,语义相近的词语,其词向量在向量空间中的距离也相近。这使得我们可以通过计算词向量之间的距离来衡量词语之间的语义相似性。
词嵌入跟前面的 Tokenize 有什么区别?Tokenize 也是一种将词语转化为计算机可以理解的数值关系。
Tokenize 是基于词汇表,对自然语言进行编码。这种编码不带有语义信息。而词嵌入,是对编码后的 Token 经过 Embedding 层大量语料的训练,得到对应的词向量。经过语料训练后,词向量中带有语义信息。
语义的一种体现是,两个词向量之间的距离,表示了他们之间的相关性。最经典的案例是,词向量还有一个神奇的特性:它不仅可以反映语义上的相似性,还能利用两个向量的差来反映语义中的抽象关系。例如,词向量有一个著名的公式:女人 - 男人 = 皇后 - 国王。
Step8:BigramLanguageModel V1 训练
使用如下代码对模型进行一万次训练:
# create a PyTorch optimizer
optimizer = torch.optim.AdamW(m.parameters(), lr=1e-3)
from tqdm import tqdm
for steps in tqdm(range(10000)): # increase number of steps for good results...
# sample a batch of data
xb, yb = get_batch('train')
# evaluate the loss
logits, loss = m(xb.to(device), yb.to(device))
optimizer.zero_grad(set_to_none=True)
loss.backward()
optimizer.step()
我用 CPU 进行训练,耗时情况如下:
100%|██████████| 10000/10000 [00:06<00:00, 1614.60it/s]
用训练后模型,生成一个长度为 100 的序列看看:
E:
T:
OLELofr myothed:
NETh:
TI
Qat herthergneYUMy;ZAm;'sinde g wals slulobus whe
KIZ!k fer
Wod he
尽管还是乱码,但是有点 Tiny Shakespeare 剧本对话的意思了。
再训练一万次(累计 2w 次):
Tof m, o, wshasoth and us un s's he teke, batt bed thares d, haurclo toun ast fen, ak,
Agh ceninstsu
还是说都不会话水平。训练十万次效果:
TORETh weir wen n n msu st'd mathithe se aieronou bino lld?
Thiso ar l l hithinanckis y'd Y:
LINodon
没觉得有什么区别……
为什么效果这么差?因为我们使用的是最简单的 BigramLanguageModel(N太小),在小数据集上,只进行了少量训练,并且我们用的 Token 是字符(字元),这些都导致训练效果不佳。
Step9:使用矩阵乘法实现累增运算
前文中多次提到累增输入,这才是 idx 在 GPT 中被处理的方式。再回顾一次:
when input is [24] the target: 43
when input is [24, 43] the target: 58
when input is [24, 43, 58] the target: 5
when input is [24, 43, 58, 5] the target: 57
when input is [24, 43, 58, 5, 57] the target: 1
when input is [24, 43, 58, 5, 57, 1] the target: 46
when input is [24, 43, 58, 5, 57, 1, 46] the target: 43
when input is [24, 43, 58, 5, 57, 1, 46, 43] the target: 39
注:以下内容对应于视频中的『The mathematical trick in self-attention』一节
GPT 中包含 Attention 自注意力机制(self-attention),简单来说,对上面的每一轮进行加权:
,输入为 ,加权为 ,输出 ,输入为 ,加权为 ,输出 ,输入为 ,加权为 ,输出
如何实现上述累增运算呢?一种直观方法是使用循环,但是这样效率低。The mathematical trick 指的就是使用一个矩阵运算来替代循环,矩阵运算效率更高,啪的一下就全算完了。
这里使用的矩阵是三角阵,下三角是权重,上三角都是 0:
权重 0 0 0
权重 权重 0 0
权重 权重 权重 0
权重 权重 权重 权重
我们以这个阵的每一行,与 idx 列向量相乘,是不是就把这一轮中的头几个元素,与权重相乘了?
为此,引入一个新的超参数 Channels:
B,T,C = 4,8,2 # batch, time, channels
x = torch.randn(B,T,C)
x.shape
"Channel" 参数指的是在神经网络,尤其是在处理自注意力(Self-Attention)机制时,数据的一个维度,它表示输入数据中的特征数量。
例如,在计算机视觉任务中,对于彩色图像,常见的通道数为3,分别代表红、绿、蓝(RGB)颜色通道。在自然语言处理(NLP)和Transformer模型的上下文中,"Channel" 通常指的是嵌入向量(embedding vector)的维度,或者说,每个单词或标记(token)被表示成的向量的大小。这些嵌入向量是高维空间中的点,每一个维度(或"channel")可以被看作是捕捉输入数据中某种特定方面的特征。
这里以通道数 C=2 作为示意。
下面介绍两种矩阵运算方法。第一种运算:
# version 2: using matrix multiply for a weighted aggregation
# 创建一个 8x8 的下三角阵
# 在下三角阵中,主对角线上方的所有元素都被设置为0
wei = torch.tril(torch.ones(T, T))
# 将每一行的元素除以该行元素的和,以确保每一行的元素和为1
# 这样做的目的是将`wei`转换为一个权重矩阵,可以用于对输入数据`x`进行加权平均。
wei = wei / wei.sum(1, keepdim=True)
# 这行代码使用矩阵乘法(`@`操作符)将权重矩阵`wei`应用于输入数据`x`
# 这实际上是对`x`的每一行进行加权平均,权重由`wei`的对应行给出。
# 结果`xbow2`的形状为`(B, T, C)`。
xbow2 = wei @ x # (B, T, T) @ (B, T, C) ----> (B, T, C)
print(xbow2)
这段代码的主要目的是创建一个下三角矩阵,并用它来对输入数据x进行加权平均。
这样,便完成了对输入序列的每轮累增处理,并在每轮累进中进行加权。下面再介绍第二种等效运算:
# 首先使用`torch.ones(T, T)`创建一个大小为`T x T`的全1矩阵
# 然后使用`torch.tril`将这个矩阵转换为下三角矩阵。
# 在下三角矩阵中,主对角线上方的所有元素都被设置为0。
tril = torch.tril(torch.ones(T, T))
# 这行代码创建了一个大小为`T x T`的全0矩阵,用于存储权重。
wei = torch.zeros((T,T))
# 这行代码使用`masked_fill`函数将`wei`中对应`tril`为0的位置填充为负无穷。
# 这样做的目的是在接下来的softmax操作中,这些位置的权重将被设置为0。
wei = wei.masked_fill(tril == 0, float('-inf'))
# 这行代码使用softmax函数将`wei`转换为一个权重矩阵,可以用于对输入数据`x`进行加权平均。
# softmax函数会将每一行的元素转换为正值,并且确保每一行的元素和为1。
wei = F.softmax(wei, dim=-1)
# 这行代码使用矩阵乘法(`@`操作符)将权重矩阵`wei`应用于输入数据`x`。
# 这实际上是对`x`的每一行进行加权平均,权重由`wei`的对应行给出。
# 结果`xbow3`的形状为`(B, T, C)`。
xbow3 = wei @ x
可以看到,这两种运算是等价的。
基础概念:Self-Attention 和 Masked Self-Attention
关于什么是 Attention,可以参见笔记《Attention》。
Self-Attention 是一种计算机制,允许模型在序列内的每个元素上计算其它元素的加权和,权重由元素之间的相似度(通常是通过点积计算)决定。这种机制使得模型能够捕捉序列内的长距离依赖关系。
Masked Self-Attention 是 Self-Attention 的一个变种,它通过应用一个掩码(mask)来限制元素间的注意力分布。在处理序列数据(如文本或时间序列)时,有时我们希望模型在计算注意力权重时只考虑当前位置之前的元素(或特定范围内的元素),以保持信息流的方向性或遵循特定的顺序。这就是掩码发挥作用的地方。
Andrej Karpathy 在视频中说道,对于 Encoder-Decoder 模型,可使用 Self-Attention,每一个输出都参考完整输入。而对于 decoder-only 模型,则使用 Masked Self-Attention,输出序列只根据当前位置之前的元素。
对于 Masked Self-Attention,上节中提到的下三角阵,实现了屏蔽当前位置之后的未来输入,从而只根据当前位置之前的元素。
Step10:实现 Masked Self-Attention
下面来实现 Masked Self-Attention。
Self Attention 的代码实现如下:
# version 4: self-attention!
torch.manual_seed(1337)
# 这两行代码首先定义了一些变量,包括批次大小(B)、时间步长(T)和通道数(C)
# 然后生成了一个随机的张量`x`,其形状为`(B, T, C)`。这是 Mock 输入
B,T,C = 4,8,32 # batch, time, channels
x = torch.randn(B,T,C)
# let's see a single Head perform self-attention
# 这些行定义了自注意力机制中的关键部分:键、查询和值。
# 每个部分都是一个线性变换,将输入的特征维度(C)转换为头大小(head_size)。
head_size = 16
key = nn.Linear(C, head_size, bias=False)
query = nn.Linear(C, head_size, bias=False)
value = nn.Linear(C, head_size, bias=False)
# 这两行代码将输入`x`通过键和查询的线性变换,得到新的键和查询。
k = key(x) # (B, T, 16)
q = query(x) # (B, T, 16)
# 这行代码计算了查询和键的点积,得到了权重矩阵`wei`。
wei = q @ k.transpose(-2, -1) # (B, T, 16) @ (B, 16, T) ---> (B, T, T)
# 这行代码创建了一个下三角矩阵。
tril = torch.tril(torch.ones(T, T))
#wei = torch.zeros((T,T))
# 这行代码将权重矩阵`wei`中对应下三角矩阵为0的位置填充为负无穷。
wei = wei.masked_fill(tril == 0, float('-inf'))
# 这行代码对权重矩阵`wei`进行了softmax操作,使得每一行的和为1。
wei = F.softmax(wei, dim=-1)
# 这行代码将输入`x`通过值的线性变换,得到新的值。
v = value(x)
# 这行代码将权重矩阵`wei`和值`v`进行矩阵乘法,得到输出`out`。
out = wei @ v
这段代码实现了一个带有掩码的自注意力(Masked Self-Attention)机制。Masked Self-Attention 允许模型在处理序列数据时,仅考虑当前位置之前的信息,常用于如生成文本的任务中,以避免未来信息的泄露。
自注意力机制的三个核心组件:查询(query)、键(key)和值(value),它们都来源于同一个输入数据 x。这里使用 nn.Linear() 对每个组件进行线性变换(映射),以生成不同的表示空间。这是实现注意力机制的标准做法,通过这种方式,可以让模型学习到如何最有效地表示数据。
如果移除用于将权重矩阵 wei 中特定位置设置为负无穷的代码行(wei.masked_fill(tril == 0, float('-inf'))),那么该实现将不再是一个带有掩码的自注意力机制,而是变回一个标准的自注意力机制。标准的自注意力允许每个序列元素“注意”序列中的所有其他元素,而不是仅仅是之前的元素。
自注意力机制的一个关键特性:查询(query)、键(key)和值(value)向量都来源于同一个输入 x。这意味着自注意力机制能够在输入数据的内部找到元素之间的关系。
注:如果将 query输入为x,key,value输入为 y,便成为另一种注意力机制——交叉注意力(cross-attention)。在交叉注意力设置中,查询(query)向量来自于一个输入(例如 x),而键(key)和值(value)向量来自于另一个不同的输入(例如 y)。这种机制常用于处理两种不同的序列,例如在机器翻译任务中,模型需要考虑源语言句子(作为 x)和目标语言句子(作为 y)之间的关系。
这段代码中,最后的几行代码(从生成下三角阵到 softmax normalize)我们已经比较熟悉了。新增的部分是引入自注意力的 query, key, value,构成了一个单头的自注意力机制。注:可以看到 Channels 变成了 32,词向量多大,这里的 C 就跟着多大。
Step11:Weight Normalization for Softmax
在原版论文的公式中,有一个分母:
Softmax函数:Softmax函数是一种将实数向量转换为概率分布的函数。对于任意实数向量,Softmax函数会压缩每个元素的范围到[0, 1],并且使得所有元素的和为1。这在多类分类问题中非常有用,特别是在模型的输出层,可以用来代表概率分布。
注意力机制中的Softmax:在注意力机制中,Softmax用于计算注意力权重,即确定在生成输出时应该给予序列中每个元素多少“注意力”。通过Softmax,模型能够决定在聚合信息时对哪些元素给予更多的重视。
Weight Normalization for Softmax:权重正规化是一种技术,用于调整权重向量的尺度,使其具有一定的统计性质(例如,使方差为1)。在注意力机制的上下文中,这是通过调整查询(query)和键(key)的点积结果来实现的,从而影响Softmax函数的输入。
为什么需要权重正规化?
- 避免Softmax饱和:如果没有正规化,当head_size(即,每个注意力头的维度)很大时,查询和键的点积结果可能会非常大,导致Softmax输入的值域过大。这会使得Softmax函数的输出变得极端,即大多数的注意力权重都集中在少数几个值上,而其他值几乎被忽略。
- 保持梯度稳定:通过控制Softmax输入的尺度,可以帮助保持梯度的稳定性,从而避免训练过程中的梯度爆炸或消失问题。
如何实现权重正规化?
- 权重正规化可以通过除以
来实现,其中 是head_size。这个操作确保了当head_size很大时,点积结果的方差大约是1,从而缩小了Softmax输入的值域。
对应的代码实现如下:
# compute attention scores ("affinities")
wei = q @ k.transpose(-2,-1) * C**-0.5 # (B, T, C) @ (B, C, T) -> (B, T, T)
Step12:单头自注意力模块
基于前面的知识储备,单头注意力模块实现如下:
class Head(nn.Module):
""" one head of self-attention """
def __init__(self, head_size):
super().__init__()
self.key = nn.Linear(n_embd, head_size, bias=False)
self.query = nn.Linear(n_embd, head_size, bias=False)
self.value = nn.Linear(n_embd, head_size, bias=False)
self.register_buffer('tril', torch.tril(torch.ones(block_size, block_size)))
self.dropout = nn.Dropout(dropout)
def forward(self, x):
B,T,C = x.shape
k = self.key(x) # (B,T,C)
q = self.query(x) # (B,T,C)
# compute attention scores ("affinities")
wei = q @ k.transpose(-2,-1) * C**-0.5 # (B, T, C) @ (B, C, T) -> (B, T, T)
wei = wei.masked_fill(self.tril[:T, :T] == 0, float('-inf')) # (B, T, T)
wei = F.softmax(wei, dim=-1) # (B, T, T)
wei = self.dropout(wei)
# perform the weighted aggregation of the values
v = self.value(x) # (B,T,C)
out = wei @ v # (B, T, T) @ (B, T, C) -> (B, T, C)
return out
其中,引入了 Dropout,在训练时随机丢掉部分权重,来提升训练效果,避免 overfiting。
Step13:多头自注意力模块
组装多个单头自注意力模块,便得到了多头自注意力模块:
class MultiHeadAttention(nn.Module):
""" multiple heads of self-attention in parallel """
def __init__(self, num_heads, head_size):
super().__init__()
self.heads = nn.ModuleList([Head(head_size) for _ in range(num_heads)])
self.proj = nn.Linear(n_embd, n_embd)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
out = torch.cat([h(x) for h in self.heads], dim=-1)
out = self.dropout(self.proj(out))
return out
多头自注意力通过并行运行多个自注意力机制来增加模型的表达能力。每个头关注输入数据的不同部分,从而能够捕获不同的信息和特征。这些不同头的输出会有不同的表示空间和维度。通过拼接这些输出,我们获得了一个综合了所有头信息的表示,但这个综合后的表示的维度会比原始输入大。
线性变换(self.proj)在这里的作用是将这个维度更大的表示压缩回原始输入数据的维度。这不仅使得多头自注意力模块的输出可以无缝地融入后续层,而且还通过这个过程整合了来自不同头的信息,增强了模型对输入数据的理解能力。
此外,线性变换还提供了额外的参数,为模型的学习提供了更多的灵活性和能力,有助于模型更好地拟合和理解数据。通过训练,这些参数可以调整以优化模型的性能,从而提高模型对于特定任务的准确性和效率。
Step14:FeedForward Layer
对多头自注意力模块进行整合:
class FeedFoward(nn.Module):
""" a simple linear layer followed by a non-linearity """
def __init__(self, n_embd):
super().__init__()
self.net = nn.Sequential(
nn.Linear(n_embd, 4 * n_embd),
nn.ReLU(),
nn.Linear(4 * n_embd, n_embd),
nn.Dropout(dropout),
)
def forward(self, x):
return self.net(x)
Step15:LayerNorm
class LayerNorm1d: # (used to be BatchNorm1d)
def __init__(self, dim, eps=1e-5, momentum=0.1):
self.eps = eps
self.gamma = torch.ones(dim)
self.beta = torch.zeros(dim)
def __call__(self, x):
# calculate the forward pass
xmean = x.mean(1, keepdim=True) # batch mean
xvar = x.var(1, keepdim=True) # batch variance
xhat = (x - xmean) / torch.sqrt(xvar + self.eps) # normalize to unit variance
self.out = self.gamma * xhat + self.beta
return self.out
def parameters(self):
return [self.gamma, self.beta]
Step16:Positional encoding
Attention 机制通过注意到序列中的其它元素实现了能力提升。但是,Attention 本身是不考虑元素在序列中的顺序的。Positional Encoding 可解决这一问题。
在许多自然语言处理任务中,词的顺序和位置对于语义的理解至关重要。然而,在使用 Transformer 模型时,由于其多头自注意力层的特性,模型对输入数据的顺序并不敏感。为了解决这个问题,位置编码(Positional Encoding)被引入 Transformer 模型中,使得模型能够理解输入数据中词的顺序和相对位置。
在视频给出了一种位置编码方法,使用 torch.arrage 与 nn.Embedding 生成位置向量:
def forward(self, idx, targets=None):
tok_emb = self.token_embedding_table(idx) # (B,T,C)
pos_emb = self.position_embedding_table(torch.arange(T, device=device)) # (T,C)
x = tok_emb + pos_emb # (B,T,C)
......
其中:
- 单词嵌入(Token Embeddings):
tok_emb = self.token_embedding_table(idx)这一行代码通过查找嵌入表将输入的单词索引idx转换成对应的嵌入向量tok_emb。嵌入表是一个预先训练好的,可以将每个唯一单词映射到一个高维空间中的向量的表。这里的(B,T,C)表示批次大小为B,序列长度为T,嵌入维度为C。 - 位置嵌入(Positional Embeddings):
pos_emb = self.position_embedding_table(torch.arange(T, device=device))这行代码生成一个位置嵌入,其中torch.arange(T)生成一个从0到T-1的序列,对应于输入序列中每个位置的索引。self.position_embedding_table是一个预先定义的嵌入表,它将这些位置索引映射到C维的向量上,这样每个位置就有了自己的位置嵌入。这个嵌入向量能够代表或编码该位置在序列中的相对或绝对位置信息。 - 合并嵌入:
x = tok_emb + pos_emb最后,通过将单词嵌入和位置嵌入相加,为每个单词生成了一个包含了位置信息的最终嵌入。这个操作确保了模型的输入既包含了单词的语义信息(通过单词嵌入),也包含了单词的位置信息(通过位置嵌入)。这样,即使在处理序列的时候,模型也能够识别出单词的顺序,从而更好地理解语言或序列数据的结构和含义。
Step17:GPT Block 组件
GPT 是由多个 Block 组件串起来的。(注,这里说的 Block 不是前面的序列切片,这里指 GPT 的组成模块)。它的构造如下:
- 加入多头自注意力
- 多头自注意力后面加 Feed Forward Layer
- 加入 residual connection(残差连接)
- 加入 LayerNorm,Pre-LayerNorm,其中,后者是在进入多头自注意力之前,就先进行层归一化
具体代码实现如下:
class Block(nn.Module):
""" Transformer block: communication followed by computation """
def __init__(self, n_embd, n_head):
# n_embd: embedding dimension, n_head: the number of heads we'd like
super().__init__()
head_size = n_embd // n_head
self.sa = MultiHeadAttention(n_head, head_size)
self.ffwd = FeedFoward(n_embd)
self.ln1 = nn.LayerNorm(n_embd)
self.ln2 = nn.LayerNorm(n_embd)
def forward(self, x):
x = x + self.sa(self.ln1(x))
x = x + self.ffwd(self.ln2(x))
return x
Step18:基于 BigramLanguageModel 魔改 GPT
接下来,我们基于已有 BigramLanguageModel 的框架,加上前面几节中的知识,魔改出 GPT:
# super simple bigram model
class BigramLanguageModelV2(nn.Module):
def __init__(self):
super().__init__()
# each token directly reads off the logits for the next token from a lookup table
self.token_embedding_table = nn.Embedding(vocab_size, n_embd)
self.position_embedding_table = nn.Embedding(block_size, n_embd)
self.blocks = nn.Sequential(*[Block(n_embd, n_head=n_head) for _ in range(n_layer)])
self.ln_f = nn.LayerNorm(n_embd) # final layer norm
self.lm_head = nn.Linear(n_embd, vocab_size)
def forward(self, idx, targets=None):
B, T = idx.shape
# idx and targets are both (B,T) tensor of integers
tok_emb = self.token_embedding_table(idx) # (B,T,C)
pos_emb = self.position_embedding_table(torch.arange(T, device=device)) # (T,C)
x = tok_emb + pos_emb # (B,T,C)
x = self.blocks(x) # (B,T,C)
x = self.ln_f(x) # (B,T,C)
logits = self.lm_head(x) # (B,T,vocab_size)
if targets is None:
loss = None
else:
B, T, C = logits.shape
logits = logits.view(B*T, C)
targets = targets.view(B*T)
loss = F.cross_entropy(logits, targets)
return logits, loss
def generate(self, idx, max_new_tokens):
# idx is (B, T) array of indices in the current context
for _ in range(max_new_tokens):
# crop idx to the last block_size tokens
idx_cond = idx[:, -block_size:]
# get the predictions
logits, loss = self(idx_cond)
# focus only on the last time step
logits = logits[:, -1, :] # becomes (B, C)
# apply softmax to get probabilities
probs = F.softmax(logits, dim=-1) # (B, C)
# sample from the distribution
idx_next = torch.multinomial(probs, num_samples=1) # (B, 1)
# append sampled index to the running sequence
idx = torch.cat((idx, idx_next), dim=1) # (B, T+1)
return idx
Step19:训练 GPT
通过如下代码训练新的 GPT 模型(重新调整了超参数):
import torch
import torch.nn as nn
from torch.nn import functional as F
# hyperparameters
batch_size = 16 # how many independent sequences will we process in parallel?
block_size = 32 # what is the maximum context length for predictions?
max_iters = 10
eval_interval = 100
learning_rate = 1e-3
device = 'cuda' if torch.cuda.is_available() else 'cpu'
eval_iters = 200
n_embd = 64
n_head = 4
n_layer = 4
dropout = 0.0
# ------------
@torch.no_grad()
def estimate_loss():
out = {}
model.eval()
for split in ['train', 'val']:
losses = torch.zeros(eval_iters)
for k in range(eval_iters):
X, Y = get_batch(split)
logits, loss = model(X, Y)
losses[k] = loss.item()
out[split] = losses.mean()
model.train()
return out
model = BigramLanguageModelV2()
m = model.to(device)
# print the number of parameters in the model
print(sum(p.numel() for p in m.parameters())/1e6, 'M parameters')
# create a PyTorch optimizer
optimizer = torch.optim.AdamW(model.parameters(), lr=learning_rate)
打印出来,我们的参数量是 0.209729 M 😂,比那些 3B、7B 小模型还小的多得多。
训练代码:
for iter in range(max_iters):
# every once in a while evaluate the loss on train and val sets
if iter % eval_interval == 0 or iter == max_iters - 1:
losses = estimate_loss()
print(f"step {iter}: train loss {losses['train']:.4f}, val loss {losses['val']:.4f}")
# sample a batch of data
xb, yb = get_batch('train')
# evaluate the loss
logits, loss = model(xb, yb)
optimizer.zero_grad(set_to_none=True)
loss.backward()
optimizer.step()
先训练 10 轮,看误差:
step 0: train loss 4.3362, val loss 4.3363
step 9: train loss 3.4326, val loss 3.4528
生成一下试试:
# generate from the model
context = torch.zeros((1, 1), dtype=torch.long, device=device)
print(decode(m.generate(context, max_new_tokens=200)[0].tolist()))
得到:
'TwlBhk; mnRjezs nZOd i Lda
Rt!dt& hie elet-fMrnoee itDot eh&YliW?Ip nF;dnfUkU& pe
bS.Msetmw KlMns
ie ?3oqwww
MKoOnledyMel mrlQ e buRvw? s,a d sor sOt ndotdcbG!
No MwHdRKWIr XX
m tIr J
ra er
这都是啥……再训练 10 轮:
step 0: train loss 3.3931, val loss 3.4245
step 9: train loss 3.2649, val loss 3.3060
生成试试:
Ie ltyluth
eu
nbrdinee safKgrl e!kteudedkaphfdurw ntsZ aoeB. Ih;l oroteuo,fat!$dRtu
mt rhe&ewe.aSd eyto
S ethmsQendn .oX.liz tHeY wutTd FWowelG -3enrn HabM sdllW eoW
Rleto t sdllgze INbKhsot dkRBL
还是不太行,加大剂量,再来 100 轮:
step 0: train loss 2.5984, val loss 2.5928
step 99: train loss 2.4671, val loss 2.4848
生成试试:
I:
Iond henorm ghe nowy orthomnt
But ad hert ait sesum uraose chrof atrve st,
Wher chot
IKI
MIONUTEUSIE;
LAJUNIEBR!LANIYOn
S:
NNI':
ABuy h seao cey wath te thath d
-riyANol al ligo ms worteme, am
明显好点了,但还是说都不会话的程度。由于我是过年回家,设备不足,只能用 CPU 炼,只能小打小闹。要知道,原始的 max_iters 都是 5000。
不过,就算是 5000,在这个玩具项目中,作用还是有限。原因在前文中已经提过,细心的同学可以往前翻翻。
本文作者:Maeiee
本文链接:Let's build GPT:from scratch, in code, spelled out.
版权声明:如无特别声明,本文即为原创文章,版权归 Maeiee 所有,未经允许不得转载!
喜欢我文章的朋友请随缘打赏,鼓励我创作更多更好的作品!
